Completeness Property Of Real Numbers Definition
Consider m n and r are three real numbers. An example is given by the real numbers which are complete but homeomorphic to the open interval 01 which is not complete.
 Rational Numbers And Irrational Numbers Rational Numbers Irrational Numbers Algebra Worksheets
Rational Numbers And Irrational Numbers Rational Numbers Irrational Numbers Algebra Worksheets
Why the set of real numbers is fundamentally dierent from the set of rational numbers.

Completeness property of real numbers definition. Axiom and the Completeness Axiom. Properties of Real Numbers. Completeness Axioms Real Numbers The Real Numbers Rare defined by Completing the rational numbers.
This means that if a number fits in the natural numbers it can also be classified as a whole number integer rational and real number. Let q be a positive integer for which 1q b a. Example of the commutative property of addition 3 5 5 3 8.
In this section we will use interval notation though we havent dened in-tervals yet. Every nonempty subset S of the real numbers that is bounded above has a supremum in mathbbR. A main reason for using real numbers is so that many sequences have limitsMore formally the reals are complete in the sense of metric spaces or uniform spaces which is a different sense than the Dedekind completeness of the order in the previous section.
Depending on the construction of the real numbers used completeness may take the form. Is the Completeness Axiom. We can concisely say that the real numbers are a complete ordered field.
An upper bound of a non-empty subset A of R is an element b R with b a for all a A. The Completeness Property is also often called the Least Upper Bound Property. We saw before that the Real numbers R have some rather unexpected properties.
In fact there are many things which it is difficult to prove rigorously. Axioms for the Real numbers. Think about the rational numbers 3 and 5 we know that we can order 3 and 5 as follows.
This contrasts with the rational numbers whose corresponding number line has a gap at each irrational value. We will use both terms in this section. Completeness is a property of the metric and not of the topology meaning that a complete metric space can be homeomorphic to a non-complete one.
Completeness is the key property of the real numbers that the rational numbers lack. There are four main properties which include commutative property associative property distributive property and identity property. The standard way of prov.
The commutative property states that the numbers on which we perform the operation can be moved or swapped from their position without making any difference to the answer. For example the set of all rational numbers the squares of which are less than 2 has no smallest upper bound Read More. In a complete ordered field.
This property holds true for addition and multiplication but not for subtraction and division. Before examining this property we explore the rational and irrational numbers discovering that both sets populate the real line more densely than you might imagine and that they are inextricably entwined. 51 Rational Numbers Definition A real number is rational if it can be written in the form p q where p and q are integers with q 6 0.
The completeness property is also known as the least upper bound property. That the real numbers contain the ratio-nal numbers as a subfield and basic properties about the behavior of and. In the decimal number system completeness is equivalent to the statement that any infinite string of decimal digits is actually a decimal representation for some real number.
Intuitively completeness implies that there are not any gaps or missing points in the real number line. Between any two real numbers there is a rational number. This means we addlimitsofsequencesof rational numbers to the field.
A sequence x n of real numbers is called a Cauchy sequence if for any ε 0 there exists an integer N possibly depending on ε. Let a and b be real numbers with a b. The Completeness Property of The Real Numbers.
We should then check that all the field axioms hold and that the ordering prop- erties persist. Details on the can be found in Which Numbers are Real. Until then the reader can use the in-.
We know that this fact is true for rational and irrational numbers. The completeness property is sometimes referred to as the Least Upper Bound Property. An element M R is a.
Basically it means that comes before on the number line and that they both come before. In real number the important mathematical property of completeness meaning that every nonempty set that has an upper bound has a smallest such bound a property not possessed by the rational numbers. It doesnt work in the other direction though.
3 comes before 5 and both numbers come before 8 35. In fact we can say that the real numbers are the complete ordered fields since it can be shown that all complete ordered fields are isomorphic. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators.
A least upper bound of a set A is a number x such that x y for all. Adding property P13 uniquely determines the real numbers. A precise denition of intervals will come at the end of the section after the least upper bound property.
Then the above properties can be described using m n and r as shown below.
 Images Tutorvista Com Cms Images 67 Real Number Properties Jpg Real Number System Number System Math Real Numbers
Images Tutorvista Com Cms Images 67 Real Number Properties Jpg Real Number System Number System Math Real Numbers
 Powerpoint Real Number System Real Number System Real Numbers Number System Worksheets
Powerpoint Real Number System Real Number System Real Numbers Number System Worksheets
 Fjhs Math 8 Decimal Form Of A Rational Number Rational Numbers Middle School Math Math Number Sense
Fjhs Math 8 Decimal Form Of A Rational Number Rational Numbers Middle School Math Math Number Sense
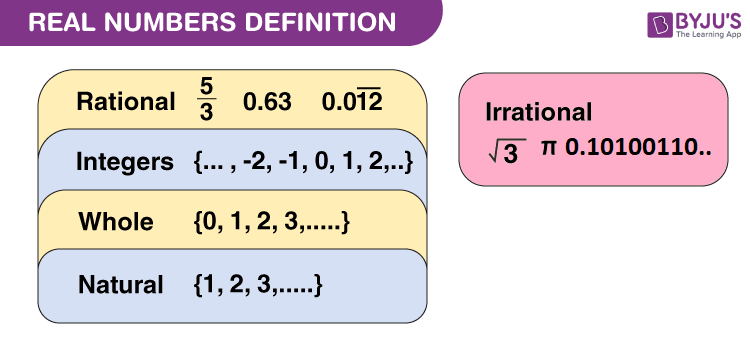 Real Numbers Definition Properties Set Of Real Numerals
Real Numbers Definition Properties Set Of Real Numerals
 A Math Hands On Model Of The Real Numbers System Includes Video Lesson Real Numbers Real Number System Math
A Math Hands On Model Of The Real Numbers System Includes Video Lesson Real Numbers Real Number System Math
 Number Sets Numbers Integers Rational Numbers And Irrational Numbers To The Set Rational Numbers Teaching Mathematics Middle School Math Resources
Number Sets Numbers Integers Rational Numbers And Irrational Numbers To The Set Rational Numbers Teaching Mathematics Middle School Math Resources
 Real Numbers Include Integers Rational Numbers Irrational Numbers But Exclude Imaginary Numbers And Infinity I Real Number System Number System Real Numbers
Real Numbers Include Integers Rational Numbers Irrational Numbers But Exclude Imaginary Numbers And Infinity I Real Number System Number System Real Numbers
 Rational Numbers Activities Rational Numbers Activities Rational Numbers Middle School Math Classroom
Rational Numbers Activities Rational Numbers Activities Rational Numbers Middle School Math Classroom
 Before Going To Discuss About The Properties Of Equalities In Math We Need To Know About Equa Math Properties Distributive Property Of Multiplication Equality
Before Going To Discuss About The Properties Of Equalities In Math We Need To Know About Equa Math Properties Distributive Property Of Multiplication Equality
 Real Number Foldable Visual Aid For Interactive Student Notebooks Interactive Student Notebooks Real Numbers Real Numbers Foldable
Real Number Foldable Visual Aid For Interactive Student Notebooks Interactive Student Notebooks Real Numbers Real Numbers Foldable
 In General Terms Real Numbers Are Those Numbers Which Do Not Considered As An Imaginary Numbers In The Mathemati Real Numbers Number Definition Maths Algebra
In General Terms Real Numbers Are Those Numbers Which Do Not Considered As An Imaginary Numbers In The Mathemati Real Numbers Number Definition Maths Algebra
 Rational And Irrational Drag And Drop Digital Activity Teaching Algebra Algebra Activities High School High School Algebra
Rational And Irrational Drag And Drop Digital Activity Teaching Algebra Algebra Activities High School High School Algebra
 Closure Property Of Addition Math Poster Properties Of Addition Math Poster Math
Closure Property Of Addition Math Poster Properties Of Addition Math Poster Math
 Math Love Algebra 2 Week 1 Inb Pictures Teaching Math Teaching Algebra Algebra
Math Love Algebra 2 Week 1 Inb Pictures Teaching Math Teaching Algebra Algebra
 The Real Number System Always Sometimes Or Never Card Sort Real Number System Real Numbers Sorting Cards
The Real Number System Always Sometimes Or Never Card Sort Real Number System Real Numbers Sorting Cards
 Properties Of Logarithms Math Poster Chart Zazzle Com Math Poster Log Math Math
Properties Of Logarithms Math Poster Chart Zazzle Com Math Poster Log Math Math
 Real Numbers Curious Concepts Precalculus 1 1 Real Numbers Real Number System Rational Numbers
Real Numbers Curious Concepts Precalculus 1 1 Real Numbers Real Number System Rational Numbers
 Math Love Algebra 1 Unit 1 Interactive Notebook Pages Teaching Algebra Teaching Math Math Notebooks
Math Love Algebra 1 Unit 1 Interactive Notebook Pages Teaching Algebra Teaching Math Math Notebooks
 Real Numbers Curious Concepts Precalculus 1 1 Real Numbers Real Number System Number System Math
Real Numbers Curious Concepts Precalculus 1 1 Real Numbers Real Number System Number System Math